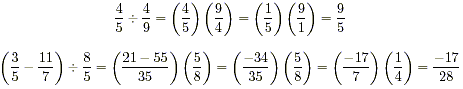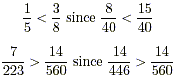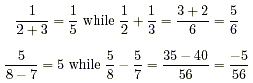Working with Fractions

Misunderstanding the rules for working with fractions is by far the most common reason for mistakes in Calculus problems. That is more than enough to justify repeating these rules.

• The best thing about fractions is being able to reduce them

Notice that all bets are off when the denominator is zero, since we’re fundamentally unable to deal with that situation. Here’s an example: “how many piles of quarters can you make with $10?” has an answer but “how many piles of nothing can you make with $10?” has no comprehensible answer. Thus, we avoid the whole problem by defining a fraction as

Remember, division by zero never makes sense, even in limits!

• To multiply fractions, we simply multiply “tops and bottoms” or numerators and denominators

Notice that and since we wrote the first two fractions, and this means by the Zero Factor Law, so the resulting fraction also makes sense.

• To divide fractions, we flip the one we’re dividing by and then multiply those

In this case, we have to assume and then again by the Zero Factor Law. However c = 0 would mean we were secretly trying to divide by , which we already know is not allowed.

• Unfortunately, addition of fractions is harder, basically because addition and division don’t go together very well. Up to reducing fractions, the rule is still pretty simple though:

We should expect to reduce this answer in most cases.

The right way to think of this rule is that we know how to add fractions with the same denominator

and we can always “unreduce” two fractions to get their product as a common denominator

.

• The rule for subtracting fractions is basically the same

although we should expect to reduce this answer in most cases.

• It is often important to find out which of two fractions is larger. However, you can always “unreduce” to get either the numerators or denominators to be the same (whichever is easier in your specific case). If the numerators are the same, the fraction with the larger denominator is smaller , because you are dividing the same numerator into more pieces. If the denominators are the same, the fraction with the larger numerator is larger , since you are dividing a bigger numerator into the same number of pieces.

• If there is a plus or minus sign in the denominator of a fraction, there is no rule telling us how to break the fraction into two reasonable pieces.

Let’s look at some examples:

Some examples of comparing two fractions:

Now some examples to show that plus/minus signs in the denominator are not something we can just break up into two pieces.