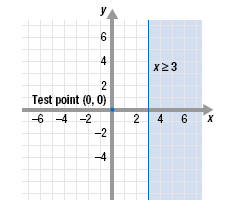
Graphing Linear Inequalities

Example 1

Graph the inequality x ≥ 3.

Solution

Step 1 Graph the equation that corresponds to the given inequality.

Graph the equation x = 3.

The graph is a vertical line through (3, 0).

Since the inequality symbol “≥” contains “equal to,” draw a solid line. The solid line shows that points on the line are solutions of the inequality.

Step 2 Use a test point NOT on the line to determine the region whose points satisfy the inequality.

The point (0, 0) is not on the line, so it can be used as a test point.

Substitute 0 for x. The resulting statement, 0 ≥ 3, is false.

Therefore, the solutions do not lie in the region containing (0, 0).

The solutions lie in the other region and on the line.

Step 3 Shade the region whose points satisfy the inequality.

Since the test point (0, 0) does NOT satisfy x ≥ 3, shade the region that does NOT include (0, 0).

This is the region to the right of the solid line, including the solid line.

Note:

A vertical line divides the xy-plane into three regions:

• points on the line

• points to the right of the line

• points to the left of the line.

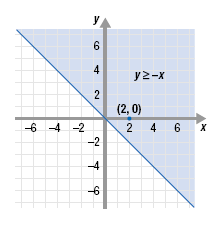
Example 2

Graph the inequality y ≥ -x.

Solution

Step 1 Graph the equation that corresponds to the given inequality.

The equation y = -x can be written as y = -1x + 0. The y-intercept is (0, 0) and the slope is -1. We use this information to graph the equation.

Since the inequality symbol “≥” contains “equal to,” draw a solid line to show that points on the line are solutions of the inequality.

Step 2 Use a test point NOT on the line to determine the region whose points satisfy the inequality.

The point (0, 0) is on the line, so we must select a different test point. Let’s use (2, 0).

In y ≥ -x, substitute 2 for x and 0 for y. The resulting statement, 0 ≥ -2, is true.

Therefore, the solutions lie in the region that contains (2, 0).

Step 3 Shade the region whose points satisfy the inequality.

Since the test point (2, 0) satisfies y ≥ -x, shade the region that contains (2, 0).

This is the region above the solid line, including the solid line.