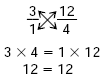Using Proportions and Cross-Multiplication

Ratios are a powerful tool in science and math. But in order to take full advantage of them, we have to do more than just calculate ratios—we have to put them to work! For example, if you have three bacteria specimens for every student in your class, you know that you will have a ratio of 3 to 1, , or 3:1. But this ratio does not tell you the total number of specimens. To find that, you need to use a proportion.

A proportion is a statement of equality between two ratios. This means that the ratios are equal. It also means that the numerator of one ratio multiplied by the denominator of the other ratio is equal to the product of the other numerator and denominator. An example looks like this:

Notice that you are multiplying across the equal sign in your proportion. This process is called cross-multiplication. Cross-multiplication is useful because if you know three of the quantities in a proportion, you can find the fourth.

PROCEDURE: To find an unknown quantity in a proportion, set up the numbers you know in equal ratios. Leave the place for the quantity you do not know empty for now. Then cross-multiply the known numerator of one ratio with the known denominator of the other. Then divide this product by your remaining known quantity. The quotient is your answer.

SAMPLE PROBLEM: Find the missing number in this proportion:

Step 1: Cross-multiply the known numerator of one ratio with the known denominator of the other ratio.

Step 2: Divide this product with your remaining known quantity.

The missing number in the proportion is 25;