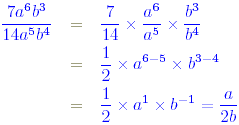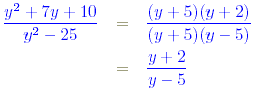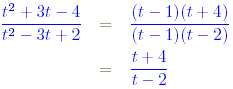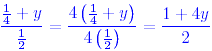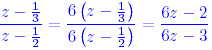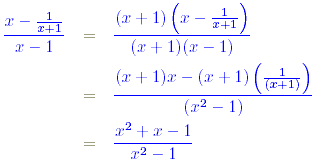|
Algebraic FractionsAlgebraic fractions have properties which are the same as those for numerical fractions, the only difference being that the the numerator (top) and denominator (bottom) are both algebraic expressions. Example 1 Simplify each of the following fractions.
Solution
N.B. The cancellation in (b) is allowed since x is a common factor of the numerator and the denominator . Sometimes a little more work is necessary before an algebraic fraction can be reduced to a simpler form. Example 2 Simplify the algebraic fraction
Solution In this case the numerator and denominator can be factored into two terms, thus
With this established the simplification proceeds as follows:
Exercise 1 Simplify each of the following algebraic fractions. (a) (b) Solution (a) The fraction is
Thus
(b) In this case, some initial factorisation is needed.
Thus
where the factor ( y + 5) has been cancelled.
Quiz Which of the following is a simplified version of
Solution The numerator and denominator respectively factorise as
so that
where the factor ( t - 1) has been cancelled from the first equation.
So far, simplification has been achieved by cancelling common factors from the numerator and denominator. There are fractions which can be simplified by multiplying the numerator and denominator by an appropriate common factor, thus obtaining an equivalent, simpler expression. Example 3 Simplify the following fractions.
Solution (a) In this case, multiplying both the numerator and the denominator by 4 gives:
(b) To simplify this expression, multiply the numerator and denominator by {\f2 x. Thus
Exercise 2 Simplify each of the following algebraic fractions. (a) (b) Solution (a) The fraction is simplified by multiplying both the numerator and the denominator by 2 .
(b) In this case, since the numerator contains the fraction 1/3 and the denominator contains the fraction 1/2 , the common factor needed is 2 × 3 = 6 . Thus
Quiz Which of the following is a simplified version of
Solution For
|
|


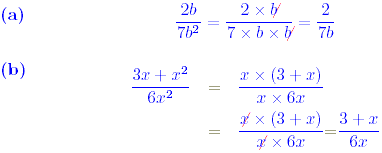
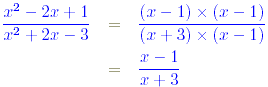 (cancelling (x-1))
(cancelling (x-1))