Simplifying Rational Expressions
After studying this lesson, you will be able to:
- Simplify rational expressions.
A rational expression is a fraction that
contains at least one variable.
There are basically 2 steps to simplify a rational expression
:
1. Factor the numerator and the denominator
2. Cancel
** Only a binomial can cancel a binomial.
** Never cancel part of a binomial or part of a trinomial. You
can cancel part of a monomial.
I. Simplifying Monomials:
Example 1
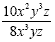
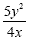
|
This is actually a review.
We already know how to simplify monomials. First,
cancel or reduce the coefficients. 10 and 8 reduces to 5
and 4
Second, divide the variables. Remember to subtract
exponents when dividing.
This is the simplified expression.
|
Example 2
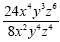
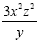
|
This is actually a review.
We already know how to simplify monomials. First,
cancel or reduce the coefficients. 24 and 8 reduces to 3
and 1
Second, divide the variables. Remember to subtract
exponents when dividing.
This is the simplified expression.
|
II. Dividing by a Monomial
Example 3
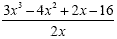 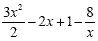
|
Divide each term in the numerator by 2x
This is the simplified expression.
|
Example 4
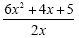 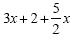
|
Divide each term in the numerator by 2x
This is the simplified expression.
|
Example 5
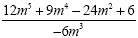 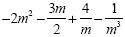
|
Divide each term in the numerator by 6 This
is the simplified expression.
|
III. Dividing by a Binomial or Trinomial
Example 6
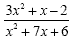 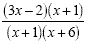
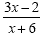
|
Factor the numerator and the
denominator.
Cancel the binomials that are identical. (x+1) cancels
(x+1)
Do not cancel the remaining x's... never cancel part
of a binomial
|
Example 7
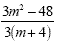 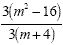
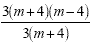
|
Factor the numerator and the
denominator.
Factor Completely
Cancel the 3's and cancel (m+4)
|
Example 8
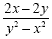 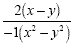
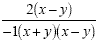
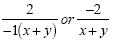
|
Factor the numerator and the
denominator.
Factor out 2 in the numerator and -1 in the
denominator
Factor Completely
Cancel out ( x - y )
|
| 
