	Algebra Tutorials!

	Thursday 21st of November



	Home
	Scientific Notation
	Notation and Symbols
	Linear Equations and Inequalities in One Variable
	Graphing Equations in Three Variables
	What the Standard Form of a Quadratic can tell you about the graph
	Simplifying Radical Expressions Containing One Term
	Adding and Subtracting Fractions
	Multiplying Radical Expressions
	Adding and Subtracting Fractions
	Multiplying and Dividing With Square Roots
	Graphing Linear Inequalities
	Absolute Value Function
	Real Numbers and the Real Line
	Monomial Factors
	Raising an Exponential Expression to a Power
	Rational Exponents
	Multiplying Two Fractions Whose Numerators Are Both 1
	Multiplying Rational Expressions
	Building Up the Denominator
	Adding and Subtracting Decimals
	Solving Quadratic Equations
	Scientific Notation
	Like Radical Terms
	Graphing Parabolas
	Subtracting Reverses
	Solving Linear Equations
	Dividing Rational Expressions
	Complex Numbers
	Solving Linear Inequalities
	Working with Fractions
	Graphing Linear Equations
	Simplifying Expressions That Contain Negative Exponents
	Rationalizing the Denominator
	Decimals
	Estimating Sums and Differences of Mixed Numbers
	Algebraic Fractions
	Simplifying Rational Expressions
	Linear Equations
	Dividing Complex Numbers
	Simplifying Square Roots That Contain Variables
	Simplifying Radicals Involving Variables
	Compound Inequalities
	Factoring Special Quadratic Polynomials
	Simplifying Complex Fractions
	Rules for Exponents
	Finding Logarithms
	Multiplying Polynomials
	Using Coordinates to Find Slope
	Variables and Expressions
	Dividing Radicals
	Using Proportions and Cross
	Solving Equations with Radicals and Exponents
	Natural Logs
	The Addition Method
	Equations

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Rational Exponents

Before we rewrite an exponential expression as a radical, we must make sure that the rational exponent is reduced to lowest terms.

Example 1

Simplify and write using only positive exponents: w^1/3 Â· w(^-3/2) = w^1/6

Solution

Each factor has the same base, w.

Therefore, add the exponents and keep w as the base.

Write each fraction with the LCD, 6.

Add the exponents.

Simplify.

w^1/3 Â· w(^-3/2) = w^1/6

= w^{1/3 + (-3/2) + 1/6}

= w^{2/6 - 9/6 + 1/6}

= w^-6/6

= w^-1

Use

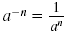to write the expression using a positive exponent.

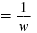Therefore,

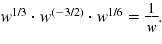
Example 2

Simplify and write using only positive exponents:

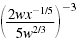
Solution

There is more than one way to start simplifying.

We begin with the Power of a Quotient Property.
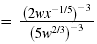Use the Power of a Product Property to raise each factor to the power -3.
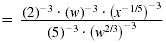Use the Power of a Power Property.
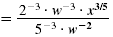Use the following to write the coefficients with positive exponents:
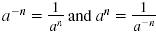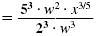Evaluate the coefficients and simplify

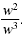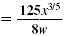So,

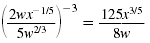
Note:

We could use radical notation to write
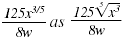