Solving Equations with Radicals and Exponents
In the next example the even-root property is used to solve some equations that
are a bit complicated.
Example 1
Using the even-root property
Solve each equation.
a) (x - 3)2 = 4
b) 2(x - 5)2 - 7 = 0
c) x4 - 1 = 80
Solution
| a) (x - 3)2 = 4 |
|
|
|
|
| x - 3 = 4 |
or |
x - 3 |
= -2 |
Even-root property |
| x = 5 |
or |
x |
= 1 |
Add 3 to each side. |
The solution set is {1, 5}.
| b) 2(x - 5)2 - 7 |
= 0 |
|
|
|
|
| 2(x - 5)2 |
= 7 |
|
|
|
Add 7 to each side. |
| (x - 5)2 |
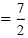 |
|
|
|
Divide each side by 2. |
| x - 5 |
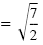 |
or |
x - 5 |
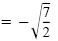 |
Even-root property |
| x |
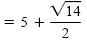 |
or |
x |
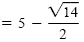 |
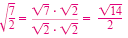 |
| x |
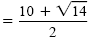 |
or |
x |
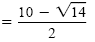 |
|
The solution set is
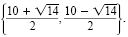
| c) x4 - 1 |
= 80 |
| x4 |
= 81 |
| x |
= ±
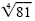 =
± 3 =
± 3 |
The solution set is {-3, 3}.
You probably know hou to solve quadratic equations by factoring. The quadratic
equations that we encounter in this chapter can be solved by using the even-root property as in parts (a) and (b) of Example
1. In the future you will learn general
methods for solving any quadratic equation.
|