Multiplying Radical Expressions
We can multiply radicals provided they have the same index. To multiply
the radicals, we multiply their radicands. The resulting radical has the
common index.
| For example, let’s find this product:
|
 |
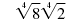| We multiply the radicands.
|
 |
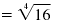| Finally, we simplify. |
= 2 |
If the expressions being multiplied contain factors that are not under a
radical symbol, multiply those factors. Then multiply the radicands of
radicals that have the same index.
| For example, let’s find this product:
|
 |
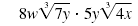| Multiply 8w by 5y. Multiply 7y by 4x.
|
 |
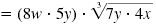| Simplify. |
 |
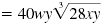In the following multiplication problem, we use the Distributive Property
to remove the parentheses.
| Find this product:
|
 |
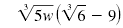Distribute
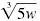 to each term
inside the parentheses.
|
 |
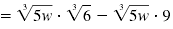| Simplify. |
 |
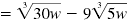Example 1
Multiply and simplify:
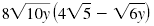
| Solution |
 |
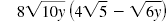Distribute
 |
 |
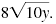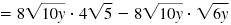| Multiply. |
 |
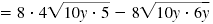| Factor each radicand.
Use perfect square
factors when possible. |
 |
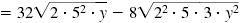| Write each radical as a
product of radicals. Place
each perfect square under
its own radical symbol.
|
 |
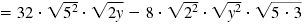| Simplify each radical.
|
 |
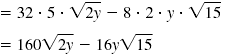| Thus, |
 |
|
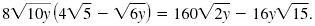