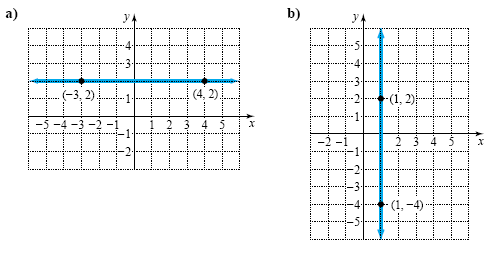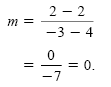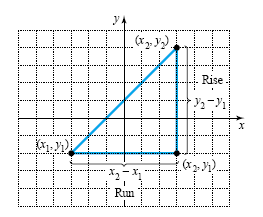
Using Coordinates to Find Slope

We can obtain the rise and run from a graph, or we can get them without a graph by subtracting the y-coordinates to get the rise and the x-coordinates to get the run for two points on the line. See the figure below.

Slope Using Coordinates

The slope m of the line containing the points (x₁, y₁) and (x₂, y₂) is given by

  , provided that x₂ - x₁ ≠ 0.

Example 1

Finding slope from coordinates

Find the slope of each line.

a) The line through (2, 5) and (6, 3)

b) The line through (-2, 3) and (-5, -1)

c) The line through (-6, 4) and the origin

Solution

a) Let (x₁, y₁) = (2, 5) and (x₂, y₂) = (6, 3). The assignment of (x₁, y₁) and (x₂, y₂) is arbitrary.

b) Let (x₁, y₁) = (-5, -1) and (x₂, y₂) = (-2, 3):

c) Let (x₁, y₁) = (0, 0) and (x₂, y₂) = (-6, 4):

Caution

Do not reverse the order of subtraction from numerator to denominator when finding the slope. If you divide y₂ - y₁ by x₁ - x₂, you will get the wrong sign for the slope.

Example 3

Slope for horizontal and vertical lines

Find the slope of each line.

Solution

a) Using (-3, 2) and (4, 2) to find the slope of the horizontal line, we get

b) Using (1, -4) and (1, 2) to find the slope of the vertical line, we get x₂ - x₁ = 0. Because the definition of slope using coordinates says that x₂ - x₁ must be nonzero, the slope is undefined for this line.

Helpful Hint

Think about what slope means to skiers. No one skis on cliffs or even refers to them as slopes.

Since the y-coordinates are equal for any two points on a horizontal line, y₂ - y₁ = 0 and the slope is 0. Since the x-coordinates are equal for any two points on a vertical line, x₂ - x₁ = 0 and the slope is undefined.

Horizontal and Vertical Lines

The slope of any horizontal line is 0.

Slope is undefined for any vertical line.

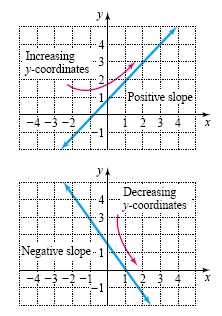
Caution

Do not say that a vertical line has no slope because “no slope” could be confused with 0 slope, the slope of a horizontal line.

As you move the tip of your pencil from left to right along a line with positive slope, the y-coordinates are increasing. As you move the tip of your pencil from left to right along a line with negative slope, the y-coordinates are decreasing. See the following figure.