Graphing Parabolas
Standard form for a Quadratic Equation:
y = ax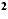 + bx + c, where a + bx + c, where a 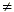 0 0
Terms:
Parabola: U-shaped graph formed by quadratic
functions.
Quadratic Term: ax
Concave Upward: a parabola that opens upward
(coefficient is positive)
Concave Downward: a parabola that opens
downward (coefficient is neg)
Vertex of a parabola: the highest point on a
concave down parabola or lowest point on a concave up parabola.
Axis of symmetry: the vertical line that
passes through vertex in a parabola.
The effects of coefficients on a quadratic system:
If a > 0 then the graph is concave upward.
If a > 0 then the graph is concave downward.
If |a| > 1 then the graph is narrower then when a = 1.
If |a| < 1 then the graph is wider then when a = 1.
c is the y -coordinate of the y -intercept of the graph.
the x -coordinate of the vertex is 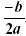
The axis of symmetry is the line graphed by 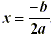 |