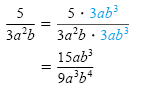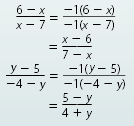|
Building Up the DenominatorOnly rational expressions with identical denominators can be added or subtracted. Fractions without identical denominators can be converted to equivalent fractions with a common denominator by reversing the procedure for reducing fractions to its lowest terms. This procedure is called building up the denominator. Consider converting the fraction
Example 1 Building up the denominator Convert each rational expression into an equivalent rational expression that has the indicated denominator.
Solution a) Factor 42 as 42 = 2 · 3 · 7, then multiply the numerator and denominator of
b) Because 9a3b4 = 3ab3 · 3a2b, we multiply the numerator and denominator by 3ab3:
When building up a denominator to match a more complicated denominator, we factor both denominators completely to see which factors are missing from the simpler denominator. Then we multiply the numerator and denominator of the simpler expression by the missing factors.
Helpful hint Notice that reducing and building up are exactly the opposite of each other. In reducing you remove a factor that is common to the numerator and denominator, and in building-up you put a common factor into the numerator and denominator.
Example 2 Building up the denominator Convert each rational expression into an equivalent rational expression that has the indicated denominator.
Solution a) Factor both 2a - 2b and 6b - 6a to see which factor is missing in 2a - 2b. Note that we factor out -6 from 6b - 6a to get the factor a - b:
Now multiply the numerator and denominator by the missing factor, -3:
b) Because x2 + 7x + 12 = (x + 3)(x + 4), multiply the numerator and denominator by x + 4:
Helpful hint Multiplying the numerator and denominator of a rational expression by -1 changes the appearance of the expression:
|
into an equivalent fraction with a denominator
of 51. Any fraction that is equivalent to
by the missing factors, 2 and 3:
|