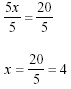Equations

An equation is a statement in which one expression is equal to another.

Examples:

24 - x + 6 = 17 or 4y + 2 = 8y - 3

We can use equations to give us information about unknown numbers as we did in the fill- in equations at the top. We call this solving for a variable. If we are asked to solve for x in the equation:

5x = 20

Then we would answer x = 4. (Remember x in this case is just an unknown number, not multiply).

Now think about what you just did to solve for x. You probably divided 20 by 5. You reversed the arithmetic shown in the equation. How does algebra help you do this work? You divide both sides of the equation by the same amount, choosing a value to simplify the arithmetic. Let’s divide both sides by 5:

Think of the equals sign ‘=’ as a balance. You can modify one side however you want, as long as you change the other side in the exact same way to keep it in balance:

· You can multiply (or divide) both sides by the same number or expression.

· You can add (or subtract) both sides by the same number or expression.

· You can even square (or use an exponent or square root) on both sides.

· You can add (or multiply) a variable on both sides, as long as it is the same variable.

· You can swap sides across the equals sign: a + b = x is the same as x = a + b.

The only thing you are not allowed to do is divide by zero. Please note there is an implied parenthesis around each side of an equation. So whatever you do must apply to everything.

Solving for a Variable

A common use for algebra is solving for one variable in an equation. You solve it by applying the same operation to both sides of the equation, to simplify it until the variable is alone on one side and the answer is on the other.

Example:

Solve for n: 9 - 5 = n

Solution:

We prefer to write it so the variable is on the left: n = 4

The key point to “solve for a variable” is to work backwards through the equation. The goal is to manipulate the equation to get the unknown variable by itself on one side of the equation. It takes some creativity and work to figure out how to simplify.

Example:

Solve for x : 5x - 6 = 19

Solution:

Check:

Put 5 into original problem: 5 • 5 - 6 = 19? Yes!

The variable itself can be operated upon, just like any other part of the equation. For example, the variable might begin at some unusual place. You can add, subtract, multiply and divide it like the other parts.

Example:

Solve for x :

Solution:

Multiply both sides by x: or:

3x = 54

Finally, this looks more familiar.

Divide both sides by 3:  or:

Note that using exponents (such as squaring) affects the whole expression on each side. You can’t just, say, use the square root on a part of one side.

Example:

Solve for x : x² + 16 = 25

Solution:

Take the square root:

  Right!

Wrong!