Simplifying Radicals Involving Variables

To simplify radicals involving variables, we must recognize exponential expressions that are perfect squares, perfect cubes, and so on. The expressions x², w⁴, y⁸, z¹⁴, and x⁵⁰ are perfect squares because they are squares of variables with integral powers. Any even power of a variable is a perfect square. If we assume the variables represent positive numbers, we can write

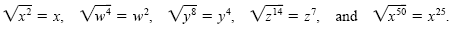
Helpful hint

If you use exponential notation, then it is clear why the square root takes half of the exponent:

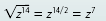
Note that when we find the square root, the result has one-half of the original exponent.

Example 1

Radicals with variables

Simplify each expression. Assume all variables represent positive real numbers.

Solution

a) Use the product rule to place all perfect squares under the first radical symbol and the remaining factors under the second:

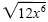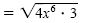		Factor out the perfect squares.
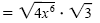		Product rule for radicals

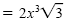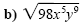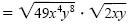		Product rule for radicals
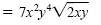