Finding Logarithms
You can find the value of some logarithms by first writing them in
exponential form. Once the equation is in exponential form, you can solve
it using the Principle of Exponential Equality.
Note:
Recall that the Principle of Exponential
Equality states that if
bx = by, then
x = y.
Here, b > 0 and b ≠ 1.
Example 1
Find log232.
Solution
| Let x equal log232 to create an equation.
Rewrite in exponential form.
Rewrite 32 as 25.
Use the Principle of Exponential Equality. |
log232 = x
2x = 32
2x = 25
x = 5 |
So, log232 = 5.
Here is a check:
Is log232 = 5 ?
Is 25 = 32 ?
Is 32 = 32 ? Yes
Example 2
Find log51.
Solution
| Let x equal log51 to create an equation.
Rewrite in exponential form.
Rewrite 1 as 50.
Use the Principle of Exponential Equality.
|
log51 = x
5x = 1
5x = 50
x = 0 |
Thus, log51 = 0.
Note:
Sometimes one side of an exponential
equation cannot be easily rewritten as a
power with the same base as the other
side. Later, you will learn how to solve
such equations.
Example 3
Find
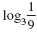
Solution
|
Let x equal
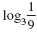 to create an equation. to create an equation.
Rewrite in exponential form.
Rewrite
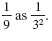
Write the right side as 3-2.
Use the Principle of Exponential Equality.
|
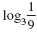 = x
= x
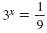
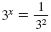
3x = 3-2
x = -2 |
So,
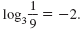
Note:
Recall the defination of a negative
exponent:
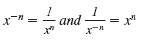
Example 4
Find log 1/2 8.
Solution
| Let x equal log 1/2 8 to create an equation.
Rewrite in exponential form.
Rewrite
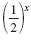 as 2-x and 8 as 23.
as 2-x and 8 as 23.
Use the Principle of Exponential Equality.
Multiple or divide both sides by -1. |
log 1/2 8 = x
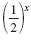 = 8
= 8
2-x = 23
-x = 3
x = -3 |
Therefore, log 1/2 8 = -3.
Note:
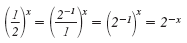 |