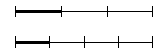|
Multiplying Two Fractions Whose Numerators Are Both 1Key Idea To multiply two fractions whose numerators are both 1, multiply the denominators and keep the numerator equal to 1.
Example 1
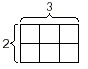
Why Does This Procedure Work?Recall that one way to model the multiplication of two whole numbers is to draw a rectangle whose length and width are the two numbers. After dividing the rectangle into unit squares, counting the unit squares gives the product of the two whole numbers. For example, consider the product 2 × 3 modeled below.
The model shows that 2 × 3 = 6. Modeling the product of two
fractions is slightly different. Begin with two segments of the
same length. Divide one segment into the number of equal parts
indicated by the denominator of the first fraction. Divide the
other segment into the number of equal parts indicated by the
denominator of the second fraction. Suppose that we want to
multiply
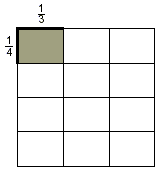
Next, we use the segments as two of the adjacent sides of a square. The marks on the segments are used to divide the square into smaller regions that are all the same size. Finally, we shade the smaller region formed by the two darkened parts of the segments.
The shaded region represents the product of the fractions. It
is one of the 12 regions of equal size into which the square is
divided. Since each side of the square represents a length of 1,
the square has an area of 1 square unit. Therefore, the shaded
region represents the fraction
|
and 
. Divide one segment
into 3 equal parts and the other into 4 equal parts. Since the
numerator of each fraction is 1, darken one of the parts of each
segment. This is shown in the figure below. 
. The model shows that 
.
|