Solving Quadratic Equations
Solving by extracting square roots
EXAMPLE:
Solve by extracting square roots
a: Solve 5x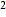 = 500 = 500
First divide both sides by 5! Then notice that the equation
only involves two terms! Also notice that the value left on the
right hand side of the equation is a perfect square number!
5x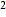 = 500 Given equation = 500 Given equation
x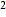 = 100 Divide by 5 = 100 Divide by 5
Thus x = ± 10 meaning x can be +10 or x can be -10!
b: Solve x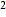 = 7 = 7
Notice that the equation only involves two terms! Also notice
that the value left on the right hand side of the equation is NOT
a perfect square number! So what !!! You can still solve this by
extracting square roots.
x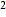 = 7 = 7
So x = ± 7
c: Solve (x- 2)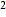 = 64 = 64
METHOD 1: Notice that the left hand side of
the equation is still a squared term. It just happens to be x -2!
It can be solved by taking the square root of both sides as
follows:
(x- 2)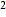 = 64 = 64
So x - 2 = ±8
Thus x - 2 = 8 or x - 2 = -8
x = 10 or x = -6
METHOD 2: Clear the parentheses, collect like
terms on left, set = 0, factor!
(x- 2)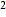 = 64 = 64
x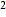 -4x + 4 = 64 -4x + 4 = 64
x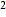 -4x + 4 - 64 = 0 -4x + 4 - 64 = 0
x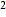 -4x - 60 = 0 -4x - 60 = 0
(x - 10)(x + 6) = 0
Either x - 10 = 0 or x + 6 = 0
x = 10 or x = -6 |