Simplifying Square Roots That Contain Variables
Next we will simplify a square-root radical whose radicand contains a
variable.
Let’s look at these examples.
If x is a nonnegative real number, then:
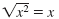 since
x · x = x2 since
x · x = x2 |
|
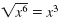 since (x3)2 = x6
since (x3)2 = x6 |
Notice that
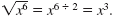 |
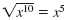 since (x5)2 = x10
since (x5)2 = x10 |
Notice that
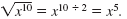 |
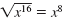 since
(x8)2 = x16 since
(x8)2 = x16 |
Notice that
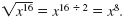 |
In each example, the exponent of the variable in the simplified expression
is one-half the exponent of the variable in the radicand.
If the power of x in the radicand is not a multiple of 2, we rewrite the
radicand as a product of x1 and an even power of x.
For example, let’s simplify
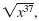 where
x is a nonnegative real number. where
x is a nonnegative real number.
|
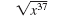 |
| Write x37 as x36
· x1. |
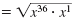 |
Write
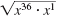 as the product of two radicals. as the product of two radicals.
|
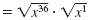 |
| Simplify. |
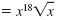 |
In the remainder of this Topic, we will assume that each variable under a
radical represents a nonnegative real number.Be careful:
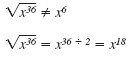
If x is negative, then
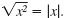
For example, if x = -3:
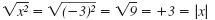
|