Raising an Exponential Expression to a Power
An expression such as (x3)2 consists of the exponential expression x3 raised to the
power 2. We can use known rules to simplify this expression.
| (x3)2 |
= x3 · x3 |
Exponent 2 indicates two factors of x3. |
| |
= x6 |
Product rule: 3 + 3 = 6 |
Note that the exponent 6 is the product of the exponents 2 and 3. This example
illustrates the power of a power rule.
Power of a Power Rule
If m and n are any integers and a ≠ 0, then
(am)n = amn.
Example
Using the power of a power rule
Use the rules of exponents to simplify each expression. Write the answer with
positive exponents only. Assume all variables represent nonzero real numbers.

Solution
| a) (23)5 = 215 |
Power of a power rule |
| b) (x2)-6 |
= x-12 |
Power of a power rule |
| |
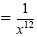 |
Definition of a negative exponent |
| c) 3(y-3)-2y-5 |
= 3y6y-5 |
Power of a power rule |
| |
= 3y |
Product rule |
d)
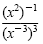 |
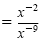 |
Power of a power rule |
| |
= x7 |
Quotient rule |
|